回归与梯度下降
回归在数学上来说是给定一个点集,能够用一条曲线去拟合之,如果这个曲线是一条直线,那就被称为线性回归,如果曲线是一条二次曲线,就被称为二次回归,回归还有很多的变种,如 locally weighted 回归, logistic 回归等等,这个将在后面去讲。
用一个很简单的例子来说明回归,这个例子来自很多的地方,也在很多的 open source 的软件中看到,比如说 weka。大概就是,做一个房屋价值的评估系统,一个房屋的价值来自很多地方,比如说面积、房间的数量(几室几厅)、地 段、朝向等等,这些影响房屋价值的变量被称为特征 (feature) 。 feature 在机器学习中是一个很重要的概念,有很多的论文专门探讨这个东西。在此处,为了简单,假设我们的房屋就是一个变量影响的,就是房屋的面积。
假设有一个房屋销售的数据如下:
| 面积(m^2) | 销售价钱(万元) |
|---|---|
| 123 | 250 |
| 150 | 320 |
| 87 | 160 |
| 102 | 220 |
| … | … |
这个表类似于帝都 5 环左右的房屋价钱,我们可以做出一个图,x 轴是房屋的面积, y 轴是房屋的售价,如下:

如果来了一个新的面积,假设在销售价钱的记录中没有的,我们怎么办呢?
我们可以用一条曲线去尽量准的拟合这些数据,然后如果有新的输入过来,我们可以在将曲线上这个点对应的值返回。如果用一条直线去拟合,可能是下面的样子:
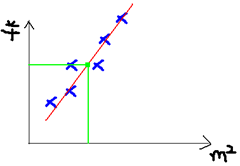
绿色的点就是我们想要预测的点。
首先给出一些概念和常用的符号,在不同的机器学习书籍中可能有一定的差别。
- 房屋销售记录表 - 训练集
(training set)或者训练数据(training data),是我们流程中的输入数据,一般称为x - 房屋销售价钱 - 输出数据,一般称为
y - 拟合的函数(或者称为假设或者模型),一般写做
y = h(x) - 训练数据的条目数
(#training set), 一条训练数据是由一对输入数据和输出数据组成的 - 输入数据的维度
(特征的个数,#features):n
下面是一个典型的机器学习的过程,首先给出一个输入数据,我们的算法会通过一系列的过程得到一个估计的函数,这个函数有能力对没有见过的新数据给出一个新的估计,也被称为构建一个模型。就如同上面的线性回归函数。
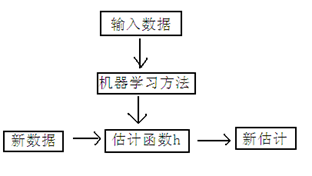
我们用 X1,X2..Xn 去描述 feature 里面的分量,比如 x1=房间的面积 , x2=房间的朝向 等等,我们可以做出一个估计函数:
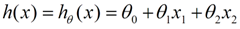
θ 在这儿称为参数,在这儿的意思是调整 feature 中每个分量的影响力,就是到底是房屋的面积更重要还是房屋的地段更重要。为了如果我们令 X0 = 1 ,就可以用向量的方式来表示了:
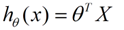
我们程序也需要一个机制去评估我们 θ 是否比较好,所以说需要对我们做出的h函数进行评估,一般这个函数称为损失函数(loss function)或者错误函数 (error function) ,描述 h 函数不好的程度,在下面,我们称这个函数为 J 函数
在这儿我们可以做出下面的一个错误函数:
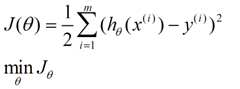
这个错误估计函数是去对 x(i) 的估计值与真实值 y(i) 差的平方和作为错误估计函数,前面乘上的 1/2 是为了在求导的时候,这个系数就不见了。
如何调整 θ 以使得 J(θ) 取得最小值有很多方法,其中有最小二乘法 (min square) ,是一种完全是数学描述的方法,在 stanford 机器学习开放课最后的部分会推导最小二乘法的公式的来源,这个来很多的机器学习和数学书 上都可以找到,这里就不提最小二乘法,而谈谈梯度下降法。
梯度下降法是按下面的流程进行的:
1)首先对θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量。
2)改变 θ 的值,使得 J(θ) 按梯度下降的方向进行减少。
为了更清楚,给出下面的图:
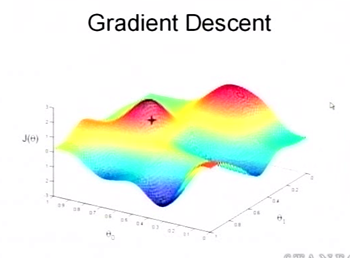
这是一个表示参数 θ 与误差函数 J(θ) 的关系图,红色的部分是表示 J(θ) 有着比较高的取值,我们需要的是,能够让 J(θ) 的值尽量的低。也就是深蓝色的部分。 θ0 , θ1 表示 θ 向量的两个维度。
在上面提到梯度下降法的第一步是给 θ 给一个初值,假设随机给的初值是在图上的十字点。
然后我们将 θ 按照梯度下降的方向进行调整,就会使得 J(θ) 往更低的方向进行变化,如图所示,算法的结束将是在 θ 下降到无法继续下降为止。
当然,可能梯度下降的最终点并非是全局最小点,可能是一个局部最小点,可能是下面的情况:
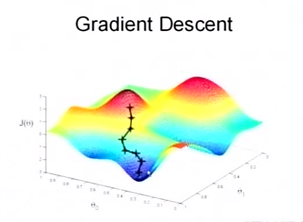
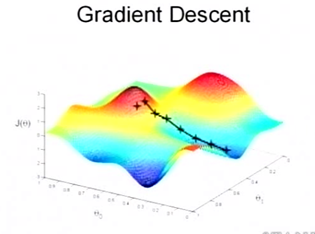
上面这张图就是描述的一个局部最小点,这是我们重新选择了一个初始点得到的,看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点
下面我将用一个例子描述一下梯度减少的过程,对于我们的函数 J(θ) 求偏导 J :(求导的过程如果不明白,可以温习一下微积分)

下面是更新的过程,也就是 θi 会向着梯度最小的方向进行减少。 θi 表示更新之前的值, - 后面的部分表示按梯度方向减少的量, α 表示步长,也就是每次按照梯度减少的方向变化多少。
一个很重要的地方值得注意的是,梯度是有方向的,对于一个向量 θ ,每一维分量 θi 都可以求出一个梯度的方向,我们就可以找到一个整体的方向,在变化的时候,我们就朝着下降最多的方向进行变化就可以达到一个最小点,不管它是局部的还是全局的。
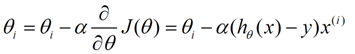
用更简单的数学语言进行描述步骤 2是这样的:
倒三角形表示梯度,按这种方式来表示, θi 就不见了。
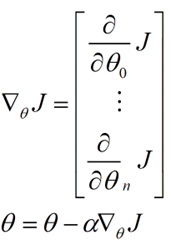
批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,其数学形式如下:
(1) 对上述的能量函数求偏导:

(2) 由于是最小化风险函数,所以按照每个参数 θθ 的梯度负方向来更新每个 θθ :
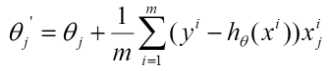
具体的伪代码形式为:
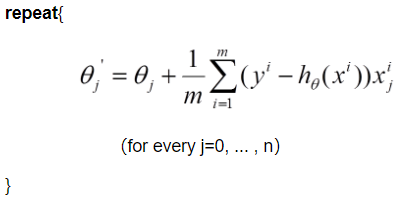
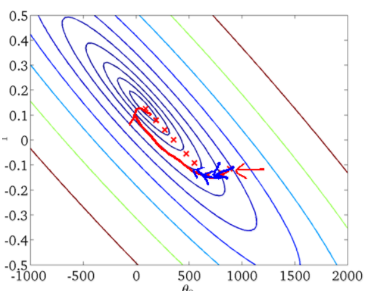
从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果样本数目 mm 很大,那么可想而知这种方法的迭代速度!所以,这就引入了另外一种方法,随机梯度下降。
- **优点:**全局最优解;易于并行实现;
- **缺点:**当样本数目很多时,训练过程会很慢。
从迭代的次数上来看, BGD 迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:
随机梯度下降法SGD
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent,简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的能量函数写为如下形式:

利用每个样本的损失函数对 θθ 求偏导得到对应的梯度,来更新 θθ :
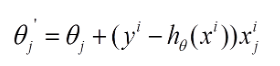
具体的伪代码形式为:

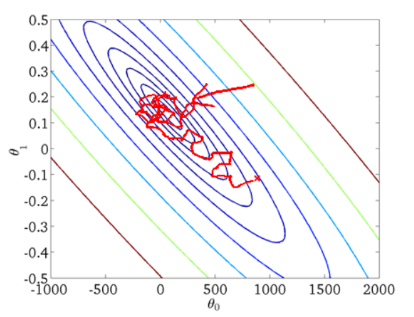
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将 theta 迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代 10 次的话就需要遍历训练样本 10 次。但是, SGD 伴随的一个问题是噪音较 BGD 要多,使得 SGD并不是每次迭代都向着整体最优化方向。
- **优点:**训练速度快;
- **缺点:**准确度下降,并不是全局最优;不易于并行实现。
从迭代的次数上来看, SGD 迭代的次数较多,在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下:
小批量梯度下降法MBGD
有上述的两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
MBGD在每次更新参数时使用 b 个样本( b 一般为 10 ),其具体的伪代码形式为:
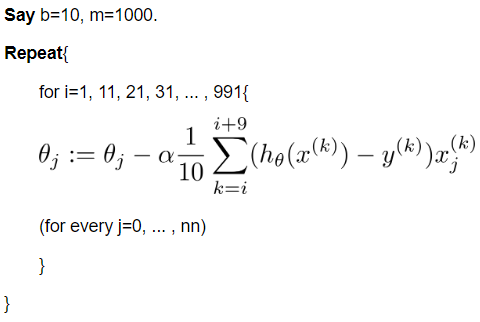
举个例子,假设我们已知门店销量如下:
| 门店数X | 实际销量Y |
|---|---|
| 1 | 13 |
| 2 | 14 |
| 3 | 20 |
| 4 | 21 |
| 5 | 25 |
| 6 | 30 |
我们如何预测门店数 X 与 Y 的关系式呢?假设我们设定为线性:Y=a0+a1X
接下来我们如何使用已知数据预测参数 a0 和 a1 呢?这里就是用了梯度下降法:



直观的表示,如下:

python 代码实现:
import sys #Training data set #each element in x represents (x1) x = [1,2,3,4,5,6] #y[i] is the output of y = theta0+ theta1 * x[1] y = [13,14,20,21,25,30] #设置允许误差值 epsilon = 1 #学习率 alpha = 0.01 diff = [0,0] max_itor = 20 error1 = 0 error0 =0 cnt = 0 m = len(x) #init the parameters to zero theta0 = 0 theta1 = 0 while 1: cnt=cnt+1 diff = [0,0] for i in range(m): diff[0]+=theta0+ theta1 * x[i]-y[i] diff[1]+=(theta0+theta1*x[i]-y[i])*x[i] theta0=theta0-alpha/m*diff[0] theta1=theta1-alpha/m*diff[1] error1=0 for i in range(m): error1+=(theta0+theta1*x[i]-y[i])**2 if abs(error1-error0)< epsilon: break print('theta0 :%f,theta1 :%f,error:%f'%(theta0,theta1,error1)) if cnt>20: print ('cnt>20') break print('theta0 :%f,theta1 :%f,error:%f'%(theta0,theta1,error1)) 结果如下:
theta0 :0.205000,theta1 :0.816667,error:1948.212261theta0 :0.379367,theta1 :1.502297,error:1395.602361theta0 :0.527993,theta1 :2.077838,error:1005.467313theta0 :0.654988,theta1 :2.560886,error:730.017909theta0 :0.763807,theta1 :2.966227,error:535.521394theta0 :0.857351,theta1 :3.306283,error:398.166976theta0 :0.938058,theta1 :3.591489,error:301.147437theta0 :1.007975,theta1 :3.830615,error:232.599138theta0 :1.068824,theta1 :4.031026,error:184.147948theta0 :1.122050,theta1 :4.198911,error:149.882851theta0 :1.168868,theta1 :4.339471,error:125.631467theta0 :1.210297,theta1 :4.457074,error:108.448654theta0 :1.247197,theta1 :4.555391,error:96.255537theta0 :1.280286,theta1 :4.637505,error:87.584709theta0 :1.310171,theta1 :4.706007,error:81.400378theta0 :1.337359,theta1 :4.763073,error:76.971413theta0 :1.362278,theta1 :4.810533,error:73.781731theta0 :1.385286,theta1 :4.849922,error:71.467048theta0 :1.406686,theta1 :4.882532,error:69.770228theta0 :1.426731,theta1 :4.909448,error:68.509764theta0 :1.445633,theta1 :4.931579,error:67.557539cnt>20theta0 :1.445633,theta1 :4.931579,error:67.557539[Finished in 0.2s]
可以看到学习率在 0.01 时, error 会正常下降。图形如下:
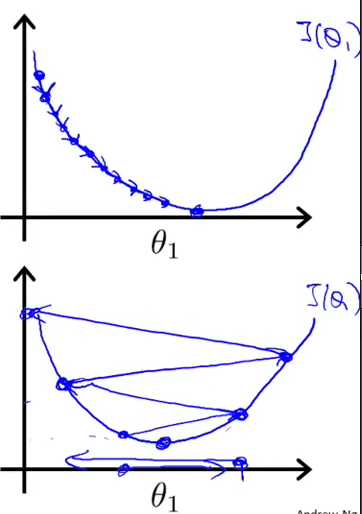
(第一张图是学习率小的时候,第二张图就是学习率较大的时候)
所以我们再调整一下新的学习率看看是否能看到第二张图:
我们将学习率调整成了 0.3 的时候得到以下结果:
theta0 :6.150000,theta1 :24.500000,error:38386.135000 theta0 :-15.270000,theta1 :-68.932500,error:552053.226569 theta0 :67.840125,theta1 :285.243875,error:7950988.401277 theta0 :-245.867981,theta1 :-1059.347887,error:114525223.507401 theta0 :946.357695,theta1 :4043.346381,error:1649619133.261223 theta0 :-3576.913313,theta1 :-15323.055232,error:23761091159.680252 theta0 :13591.518674,theta1 :58177.105053,error:342254436006.869995 theta0 :-51565.747234,theta1 :-220775.317546,error:4929828278909.234375 theta0 :195724.210360,theta1 :837920.911885,error:71009180027939.656250 theta0 :-742803.860227,theta1 :-3180105.158068,error:1022815271242165.875000 theta0 :2819153.863813,theta1 :12069341.864380,error:14732617369683060.000000 theta0 :-10699395.102930,theta1 :-45806250.675551,error:212208421856953728.000000 theta0 :40606992.787278,theta1 :173846579.256281,error:3056647245837464576.000000 theta0 :-154114007.118001,theta1 :-659792674.286440,error:44027905696333684736.000000 theta0 :584902509.168162,theta1 :2504083725.690765,error:634177359734604038144.000000 theta0 :-2219856149.407590,theta1 :-9503644836.328783,error:9134682134868024885248.000000 theta0 :8424927779.709908,theta1 :36068788150.345154,error:131575838248146814631936.000000 theta0 :-31974778105.915466,theta1 :-136890372077.920685,error:1895216599231190653730816.000000 theta0 :121352546013.825867,theta1 :519534337912.329712,error:27298674329760760684609536.000000 theta0 :-460564272592.117981,theta1 :-1971767072878.787598,error:393209736799816196514906112.000000 theta0 :1747960435714.394287,theta1 :7483365594965.919922,error:5663787744653302294061776896.000000 cnt>20 theta0 :1747960435714.394287,theta1 :7483365594965.919922,error:5663787744653302294061776896.000000 [Finished in 0.2s]
可以看到 theta0 和 theta1 都在跳跃,与预期相符。
上文使用的是批量梯度下降法,如遇到大型数据集的时候这种算法非常缓慢,因为每次迭代都需要学习全部数据集,后续推出了随机梯度下降,其实也就是抽样学习的概念。